Деление столбиком с остатком

Деление натуральных чисел с остатком: правило, примеры решений

Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах. Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания.

Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком. Приведем решение примера, так как понять суть метода проще всего на практике.

Разделим натуральное число 273844 на натуральное число 97.

Деление столбиком

Деление многозначных чисел легче всего выполнять столбиком. иначе называют деление уголком.

Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком.

Сначала записываем делимое и справа от него ставим вертикальную черту: За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту: Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное: Под делимым будут записываться промежуточные вычисления: Полностью форма записи деления столбиком выглядит следующим образом: Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению: выполняется поэтапно.

Первое, что нам требуется сделать, это определить неполное делимое.

Смотрим на первую цифру делимого: это число 7, так как оно меньше делителя, то

Как делить в столбик?

Как объяснить ребенку деление столбиком?

Деление на однозначное, двузначное, трехзначное число, деление с остатком

Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал. Содержание

1. Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
2. Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
3. Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию

Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения.

— — — Деление в столбик — подробное описание алгоритма решения задач, примеры Найти 138 Автор статьи Время на чтение: 6 минут 6 марта 2023 2117 В эпоху компьютеров и калькуляторов деление в столбик может показаться устаревшим способом.

Если вы уже немного знакомы с арифметическими действиями, то, наверное, знаете, как называются числа, с которыми придется иметь дело:

1. делимое — это то, что вам нужно разделить;
2. частное — то, что получается в итоге.
3. делитель — на него всегда делят;

В Интернете есть немало сайтов, где это действие можно выполнить с помощью онлайн-калькулятора.

Что такое деление с остатком: примеры для ребенка в 3, 4 классе

› › Как научить ребенка делению?

В результате данного математического действия, помимо целой части, остается неделимый кусок.

Приведем простой пример того, как делить с остатком: Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды.

Это и есть остаток.

Коллегия адвокатов

Введите числа и калькулятор разделит числа столбиком и отобразит подробное решение. Метод деления столбиком, позволяет упростить деления чисел.

Рассмотрим как делить в столбик на примере нахождения частного двух чисел 6344 ÷ 61. 1 Запишем числа которые будем делить следующим образом:

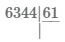
. Слева расположено делимое 6344, справа от черты делитель 61, ниже делителя будем записывать частное.

2 Найдем первую цифру частного, для этого сравниваем делитель 61 с числом состоящим из первый цифр делимого, пока не сформируем число большее или равное делителю. На первом шаге: 6 61, следовательно мы нашли третью цифру частного; записываем в частное 4=244 ÷ 61.

Мы использовали все цифры и получили что число 61 делит на цело число 6344 а частное равно 104.

3 класс: деление с остатком, примеры и пояснения

January 12, 2017 Обсудить 0 0 Чем занимается на математике 3 класс?

Деление с остатком, примеры и задачи — вот что изучается на уроках.

О делении с остатком и алгоритме таких вычислений пойдет речь в статье. Рассмотрим темы, включенные в программу, которую изучает 3 класс.

Деление с остатком выделено в специальный раздел математики. О чем идет речь? Если делимое не делится на делитель нацело, то остается остаток.

Например, делим 21 на 6. Получается 3, но в остатке остается 3. В случаях, когда во время деления остаток равен нулю, говорят о том, что произведено деление нацело.

Например, если 25 нужно поделить на 5, получается число 5.

Остаток равен нулю.Для того чтобы произвести деление с остатком, используется определенная запись.Приведем примеры по математике (3 класс). Деление с остатком в столбик можно не записывать. Достаточно записи в строчку: 13:4=3 (остаток 1) или 17:5=3 (остаток 2).Разберем все подробнее.

Совет 1: Как объяснить деление в столбик

28 апреля 2012 Автор КакПросто!

Совет 1: Как объяснить деление в столбик Деление столбиком проходят в третьем классе начальной школы.

Взрослому кажется, что ничего тут сложного нет.

Но ребенок может не понять материал на уроке или пропустить занятия из-за болезни. Тогда задача родителей – максимально понятно донести информацию до малыша, чтобы отставание в школе не усугубилось.

Проявите такт и терпение, ведь простые вещи всегда очень сложно делать в первый раз. Статьи по теме:

1. Как объяснить деление в столбик
2. Как разделить число на десятичную дробь
3. Как вычитать столбиком Вопрос «как внести изменения в коллективный договор» — 2 ответа Вам понадобится
   — ручка;- бумага для записей. Инструкция 1 Сначала проверьте навыки ребенка в умножении.

Деление с остатком. Формула деления с остатком и проверка.

» » Рассмотрим простой пример: 15:5=3 В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.

Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу: В шкафу лежало 16 игрушек.

В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?

Решение: Поделим число 16 на 5 столбиком получим: Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке.

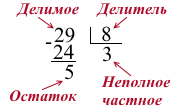
Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.

16=5⋅3+1 a=b⋅c+d a – делимое, b – делитель, c – неполное частное, d – остаток. Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется. Остаток всегда должен быть меньше делителя.

Деление с остатком

Если одно натуральное число не делится на другое нацело, можно выполнить деление с остатком.

Как и при делении нацело, числа, которые делим, называются делимое и делитель. Результат деления называется неполным частным. Число, которое остаётся от делимого в результате деления (это число меньше делителя), называется остаток.

Чтобы выполнить проверку, надо:

• Неполное частное умножить на делитель.
• К полученному произведению прибавить остаток.
• В результате должно получиться делимое.

Рассмотрим конкретные примеры деления с остатком. Примеры. Выполнить деление чисел с остатком и сделать проверку: 1) 29 : 8; 2) 613 : 6; 3) 279 : 10; 4) 784 : 23; 5) 4057 : 35; 6) 8591 : 62; 7) 52779 : 2524; 8) 15 : 79.

Решение: 1)

29 : 8 = 3 (остаток 5).